教学目标
（1）正确理解排列的意义。能利用树形图写出简单问题的所有排列；
（2）了解排列和排列数的意义，能根据具体的问题，写出符合要求的排列；
（3）掌握排列数公式，并能根据具体的问题，写出符合要求的排列数；
（4）会分析与数字有关的排列问题，培养学生的抽象能力和逻辑思维能力；
（5）通过对排列应用问题的学习，让学生通过对具体事例的观察、归纳中找出规律，得出结论，以培养学生严谨的学习态度。
教学建议
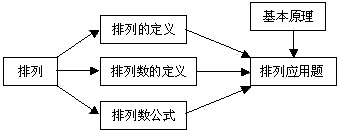
一、知识结构
二、重点难点分析
本小节的重点是排列的定义、排列数及排列数的公式，并运用这个公式去解决有关排列数的应用问题．难点是导出排列数的公式和解有关排列的应用题．突破重点、难点的关键是对加法原理和乘法原理的掌握和运用，并将这两个原理的基本思想方法贯穿在解决排列应用问题当中．
从n个不同元素中任取m（m≤n）个元素，按照一定的顺序排成一列，称为从n个不同元素中任取m个元素的一个排列．因此，两个相同排列，当且仅当他们的元素完全相同，并且元素的排列顺序也完全相同．排列数是指从n个不同元素中任取m（m≤n）个元素的所有不同排列的种数，只要弄清相同排列、不同排列，才有可能计算相应的排列数．排列与排列数是两个概念，前者是具有m个元素的排列，后者是这种排列的不同种数．从集合的角度看，从n个元素的有限集中取出m个组成的有序集，相当于一个排列，而这种有序集的个数，就是相应的排列数．
公式推导要注意紧扣乘法原理，借助框图的直视解释来讲解．要重点分析好 
的推导．
排列的应用题是本节教材的难点，通过本节例题的分析，应注意培养学生解决应用问题的能力．
在分析应用题的解法时，教材上先画出框图，然后分析逐次填入时的种数，这样解释比较直观，教学上要充分利用，要求学生作题时也应尽量采用．
在教学排列应用题时，开始应要求学生写解法要有简要的文字说明，防止单纯的只写一个排列数，这样可以培养学生的分析问题的能力，在基本掌握之后，可以逐渐地不作这方面的要求．
三、教法建议
①在讲解排列数的概念时，要注意区分“排列数”与“一个排列”这两个概念．一个排列是指“从n个不同元素中，任取出m个元素，按照一定的顺序摆成一排”，它不是一个数，而是具体的一件事；排列数是指“从n个不同元素中取出m个元素的所有排列的个数”，它是一个数．例如，从3个元素a，b，c中每次取出2个元素，按照一定的顺序排成一排，有如下几种：
ab，ac，ba，bc，ca，cb，
其中每一种都叫一个排列，共有6种，而数字6就是排列数，符号 
表示排列数．
②排列的定义中包含两个基本内容，一是“取出元素”，二是“按一定顺序排列”．
从定义知，只有当元素完全相同，并且元素排列的顺序也完全相同时，才是同一个排列，元素完全不同，或元素部分相同或元素完全相同而顺序不同的排列，都不是同一排列。叫不同排列．
在定义中“一定顺序”就是说与位置有关，在实际问题中，要由具体问题的性质和条件来决定，这一点要特别注意，这也是与后面学习的组合的根本区别．
在排列的定义中 
，如果 
有的书上叫选排列，如果 
，此时叫全排列．
要特别注意，不加特殊说明，本章不研究重复排列问题．
③关于排列数公式的推导的教学．公式推导要注意紧扣乘法原理，借助框图的直视解释来讲解．课本上用的是不完全归纳法，先推导 
， 
，…，再推广到 
，这样由特殊到一般，由具体到抽象的讲法，学生是不难理解的．
导出公式 
后要分析这个公式的构成特点，以便帮助学生正确地记忆公式，防止学生在“n”、“m”比较复杂的时候把公式写错．这个公式的特点可见课本第229页的一段话：“其中，公式右边第一个因数是n，后面每个因数都比它前面一个因数少1，最后一个因数是 
，共m个因数相乘．”这实际是讲三个特点：第一个因数是什么？最后一个因数是什么？一共有多少个连续的自然数相乘．
公式 
是在引出全排列数公式 
后，将排列数公式变形后得到的公式．对这个公式指出两点：（1）在一般情况下，要计算具体的排列数的值，常用前一个公式，而要对含有字母的排列数的式子进行变形或作有关的论证，要用到这个公式，教材中第230页例2就是用这个公式证明的问题；（2）为使这个公式在 
时也能成立，规定 
，如同 
时 
一样，是一种规定，因此，不能按阶乘数的原意作解释．
④建议应充分利用树形图对问题进行分析，这样比较直观，便于理解．
⑤学生在开始做排列应用题的作业时，应要求他们写出解法的简要说明，而不能只列出算式、得出答数，这样有利于学生得更加扎实．随着学生解题熟练程度的提高，可以逐步降低这种要求．
教学设计示例
排列
教学目标
（1）正确理解排列的意义。能利用树形图写出简单问题的所有排列；
（2）了解排列和排列数的意义，能根据具体的问题，写出符合要求的排列；
（3）会分析与数字有关的排列问题，培养学生的抽象能力和逻辑思维能力；
教学重点难点
重点是排列的定义、排列数并运用这个公式去解决有关排列数的应用问题。
难点是解有关排列的应用题。
教学过程设计
一、 复习引入
上节课我们学习了两个基本原理，请大家完成以下两题的练习（用投影仪出示）：
1．书架上层放着50本不同的社会科学书，下层放着40本不同的自然科学的书．
（1）从中任取1本，有多少种取法？
（2）从中任取社会科学书与自然科学书各1本，有多少种不同的取法？
2．某农场为了考察三个外地优良品种A，B，C，计划在甲、乙、丙、丁、戊共五种类型的土地上分别进行引种试验，问共需安排多少个试验小区？
找一同学谈解答并说明怎样思考的的过程
第1（1）小题从书架上任取1本书，有两类办法，第一类办法是从上层取社会科学书，可以从50本中任取1本，有50种方法；第二类办法是从下层取自然科学书，可以从40本中任取1本，有40种方法．根据加法原理，得到不同的取法种数是50+40=90．第（2）小题从书架上取社会科学、自然科学书各1本（共取出2本），可以分两个步骤完成：第一步取一本社会科学书，第二步取一本自然科学书，根据乘法原理，得到不同的取法种数是： 50×40=2000．
第2题说，共有A，B，C三个优良品种，而每个品种在甲
