第一课时
一、教材分析
（一）教材所处的地位和作用
“算术平均数与几何平均数”是全日制普通高级中学教科书（试验修订本·必修）数学第二册（上）“不等式”一章的内容，是在学完不等式性质的基础上对不等式的进一步研究．本节内容具有变通灵活性、应用广泛性、条件约束性等特点，所以本节内容是培养学生应用数学知识，灵活解决实际问题，学数学用数学的好素材二同时本节知识又渗透了数形结合、化归等重要数学思想，所以有利于培养学生良好的思维品质．
（二）教学目标
1．知识目标：理解两个实数的平方和不小于它们之积的2倍的重要不等式的证明及其几何解释；掌握两个正数的算术平均数不小于它们的几何平均数定理的证明及其几何解释；掌握应用平均值定理解决一些简单的应用问题．
2．能力目标：培养学生数形结合、化归等数学思想．
（三）教学重点、难点、关键
重点：用平均值定理求某些函数的最值及有关的应用问题．
难点：定理的使用条件，合理地应用平均值定理．
关键：理解定理的约束条件，掌握化归的数学思想是突破重点和难点的关键．
（四）教材处理
依据新大纲和新教材，本节分为二个课时进行教学．第一课时讲解不等式（两个实数的平方和不小于它们之积的2倍）和平均值定理及它们的几何解释．掌握应用定理解决某些数学问题．第二课时讲解应用平均值定理解决某些实际问题．为了讲好平均值定理这节内容，在紧扣新教材的前提下，对例题作适当的调整，适当增加例题．
二、教法分析
（－）教学方法
为了激发学生学习的主体意识，又有利于教师引导学生学习，培养学生的数学能力与创新能力，使学生能独立实现学习目标．在探索结论时，采用发现法教学；在定理的应用及其条件的教学中采用归纳法；在训练部分，主要采用讲练结合法进行．
（二）教学手段
根据本节知识特点，为突出重点，突破难点，增加教学容量，利用计算机辅导教学．
三、教学过程设计
6．2算术平均数与几何平均数（第一课时）
（一）导入新课
（教师活动）1．教师打出字幕（提出问题）；2．组织学生讨论，并点评．
（学生活动）学生分组讨论，解决问题．
[字幕] 某种商品分两次降价，降价的方案有三种：方案甲是第一次9折销售，第二次再8折销售；方案乙是第一次8折销售，第二次再9折销售；方案丙是两次都是 
折销售．试问降价最少的方案是哪一种？
［讨论］
①设物价为t元，三种降价方案的销售物价分别是：
方案甲： 
（元）；
方案乙： 
（元）；
方案丙： 
（元）．
故降价最少的方案是丙．
②若将问题变为第一次a折销售，第二次b折销售．显然可猜想有不等式 
成立，即 
，当 
时， 
设计意图：提出一个商品降价问题，要求学生讨论哪一种方案降价最少．学生对问题的背景较熟悉，可能感兴趣，从而达到说明学习本节知识的必要，激发学生求知欲望，合理引出新课．
（二）新课讲授
【尝试探索，建立新知】
（教师活动）打出字幕（重要不等式），引导学生分析、思考，讲解重要不等式的证明．点评有关问题．
（学生活动）参与研究重要不等式的证明，理解有关概念．
［字幕］如果 
，那么 
（当且仅当 
时取“=”号）．
证明：见课本
［点评］
①强调 
的充要条件是 
②解释“当且仅当”是充要条件的表达方式（“当”表示条件是充分的，“仅当”表示条件是必要的）．
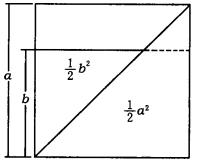
③几何解释，如图。
[字幕]定理 如果a，b是正数，那么 
（当且仅当 
时取“=”号）．
证明：学生运用“ 
”自己证明．
［点评］
①强调； 
②解释“算术平均数”和“几何平均数”的概念，并叙述它们之间的关系；
②比较上述两个不等式的特征（强调它们的限制条件）；
④几何解释（见课本）；
＠指出定理可推广为“n个（ 
）正数的算术平均数不小干它们的几何平均数”．
设计意图：加深对重要不等式的认识和理解；培养学生数形结合的思想方法和对比的数学思想，多方面思考问题的能力．
【例题示范，学会应用】
（教师活动）教师打出字幕（例题），引导学生分析，研究问题，点拨正确运用定理，构建证题思路．
（学生活动）与教师一道完成问题的论证．
［字幕］例题已知 a，b，c，d都是正数，求证： 
［分析］
①应用定理证明；
②研究问题与定理之间的联系；
③注意应用定理的条件和应用不等式的性质．
证明：见课本．
设计意图：巩固对定理的理解，学会应用定理解决某些数学问题．
【课堂练习】
（教师活动）打出字幕（练习），要求学生独立思考，完成练习；巡视学生解题情况，对正确的解法给予肯定和鼓励，对偏差给予纠正；请甲、乙两学生板演；点评练习解法．
（学生活动）在笔记本上完成练习，甲、动两位同学板演．
［字幕］练习：已知 
都是正数，求证：
（1） 
；
（2） 
设计意图：掌握定理及应用，反馈课堂教学效果，调节课堂
