教学建议
知识归纳
1．中心对称
把一个图形绕着某一点旋转
，如果它能够与另一个图形重合，那么就说这两个图形关于这个点对称，这个点叫做对称中心，两个图形关于点对称也称中心对称，这两个图形中的对应点，叫做关于中心的对称点．
中心对称的两个图形具有如下性质：（1）关于中心对称的两个图形全等；（2）关于中心对称的两个图形，对称点的连线都过对称中心，并且被对称中心平分．
判断两个图形成中心对称的方法是：如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于这一点对称．
2．中心对称图形
把一个图形绕某一点旋转
，如果旋转后的图形能够和原来的图形互相重合，那么这个图形叫做中心对称图形，这个点就是它的对称中心．
矩形、菱形、正方形、平行四边形都是中心对称图形，对角钱的交点就是它们的对称中心；圆是中心对称图形，圆心是对称中心；线段也是中心对称图形，线段中点就是它的对称中心．
知识结构
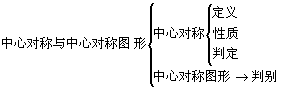
重点、难点分析：
本节课的重点是中心对称的概念、性质和作已知点关于某点的对称点.因为概念是推导三个性质的主要依据、性质是今后解决有关问题的理论依据；而作已知点关于某个点的对称点又是作中心对称图形的关键.
本节课的难点是中心对称与中心对称图形之间的联系和区别.从概念角度来说，中心对称图形和中心对称是两个不同而又紧密相联的概念.从学生角度来讲，在学习轴对称时，有相当一部分学生对轴对称和轴对称图形的概念理解上出现误点.因此本节课的难点是中心对称与中心对称图形之间的联系和区别.
教法建议
本节内容和生活结合较多，新课导入可考虑以下方法：
（1）从相似概念引入：中心对称概念与轴对称概念比较相似，中心对称图形与轴对称图形比较相似，可从轴对称类比引入，
（2）从汉字引入：有许多汉字都是中心对称图形，如“田”、“日”、“曰”、“中”、“申”、“王”，等等，可从汉字引入，
（3）从生活实例引入：生活中有许多中心对称实例和中心对称图形，如飞机的螺旋桨，风车的风轮，纽结，雪花，等等，可从生活实例引入，
（4）从商标引入：各公司、企业的商标中有许多中心对称实例和中心对称图形，如联想，联合证券，湘财证券，中国工商银行，中国银行，等等，可从这些商标引入，
（5）从车标引入：各品牌汽车的车标中有许多都是中心对称图形，如奥迪，韩国现代，本田，富康，欧宝，宝马，等等，可从车标引入，
（6）从几何图形引入：学习过的许多图形都是中心对称图形，如圆，平行四边形，矩形，菱形，正方形，等等，可从几何图形引入，
（7）从艺术品引入：艺术品中有许多都是呈中心对称或是中心对称图形，如下图，可从艺术品引入。
教学设计示例
教学目标
1．知道中心对称的概念，能说出中心对称的定义和关于中心对称的两个图形的性质。
2．会根据关于中心对称图形的性质定理2的逆定理来判定两个图形关于一点对称；会画与已知图形关于一点成中心对称的图形。
此外，通过复习图形轴对称，并与中心对称比较，渗透类比的思想方法；用运动的观点观察和认识图形，渗透旋转变换的思想。
引导性材料
想一想：怎样的两个图形叫做关于某直线成轴对称？成轴对称的两个图形有什么性质？
（帮助学生复习轴对称的有关知识，为中心对称教学作准备）
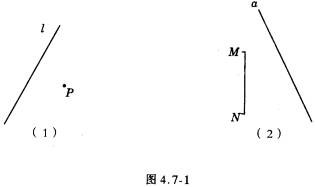
画一画：如图4.7-1(1)，已知点P和直线L，画出点P关于直线L的对称点P′；如图4.7-1(2)，已知线段MN和直线a,画出线段MN关于直线a的对称线段M′N′。
(通过画图形进一步巩固和加深对轴对称的认识)
上述问题由学生回答，教师作必要的提示，并归纳总结成下表：
width="4%" height=30> width="71%" colSpan=2 height=30>
轴对称
width="25%" height=30> width="4%" height=30>定义三要点
width="25%" height=30>1
2
3
有一条对称轴---直线
图形沿轴对折，即翻转180度
翻转后与另一图形重合
性质
width="25%" height=30>1
2
3
两个图形是全等形
对称轴是对应点连线的垂直平分线
对应线段或延长线相交，交点在对称轴上
观察与思考：图4.7-2所示的图形关于某条直线成轴对称吗？如果是，画出对称轴，如果不是，说明理由。
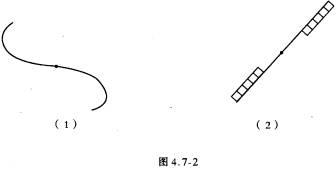
（教师把图4.7－2的两个图形制成投影片或教具，学生仔细观察后，能发现这两个图形都不是轴对称。然后，教师适时提出问题：这两个图形能不能重合？怎样才能使这两个图形重合呢？让学生观察、探究、讨论，教师可以直观地演示中心对称变换的过程，让学生发现：把其中一个图形统一特殊点旋转180度后能与另一个图形重合。）
教学设计
问题1：你能举出1～2个实例或实物，说明它们也具有上面所说的特性吗？
说明：学生自己举例有助于他们感性地认识中心对称的意义。然后，教师指出：具有这种特性的图形叫做中心对称图形，并介绍对称中心，对称点等概念。
问题2：你能给“中心对称”下一个定义吗？
说明与建议：学生下定义会有困难，教师应及时修正，并给出明确的定义，然后指出定义中的三个要点：（l）有一个对称中心——点；（2）图形绕中心旋转180度；（3）旋转后与另一图形重合。把这三要点填入引导性材料中的空表内，在顶空格内写上“中心对称”字样，以利于写“轴对称”进行比较。
练一练：在图4.7－3中，已知△ABC和△EFG关于点O成中心对称，分别找出图中的对称点和对称线段。
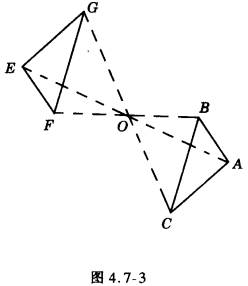
说明与建议：教师可演示△ABC绕点O旋转180度后与△EFG重合的过程，让学生说出点E和点A，点B和点F，点C和点G是对称点；线段AB和EF、线段AC和EG，线段BC和FG都是对称线段。教师还可向学生指出，图4.7－3中，点A、O、E在一条直线上，点C、O、G在一条直线上，点B、O、F在一条直线上，且AO=EO，BO=FO，CO＝GO。
问题3：从上面的练习及分析中，可以看出关于中心对称的两个图形具有哪些性质？
说明与建议：引导学生总结出关于中心对称的两个图形的性质：定理l---关于中心对称的两个图形是全等形；定理2——关于中心对称的两个图形，对称点连线都经过对称中心，并且被对称中心平分。
问题4：定理2的题设和结论各是什么？试说出它的逆命题。
说明与建议：学生解答此题有困难，教师要及时引导。特别是叙述命题时，学生常常照搬“对称点”、“对称中心”这些词语，教师应指出：由于没有“两个图形关于中心对称”的前提，所以不能使用“对称点”、“对称中心”这样的词语，而要改为“对应如”、“某一点”。最后，教师应完整地叙述这个逆命题---如果两个图形的对应点连线都经过某一点，并且被这一点平分，那么这两个图形关于点对称。
问题5：怎样证明这个逆命题是正确的？
说明与建议：证明过程应在教师的引导下，师生共同完成。由已知条件——对应点的连线都经过某一点，并且被这一点平分，可以知道
